Measurements Great Pyramid and Giza Layout
b = (10/pi – 1) * b3 where b is the base of the Great Pyramid P1, and b3 is the base of the third pyramid P3
The measurements of the pyramids and their layout are all taken from the online version of the survey by Flinders Petrie, and they’re all in inches. See http://www.ronaldbirdsall.com/gizeh/
Here there are some good aerial photos
https://commons.wikimedia.org/wiki/Category:Aerial_photographs_of_Giza_pyramid_complex#/media/File:Giza-pyramids-complex.JPG
The Blue Lines and The Red Rectangle
———————————————————-
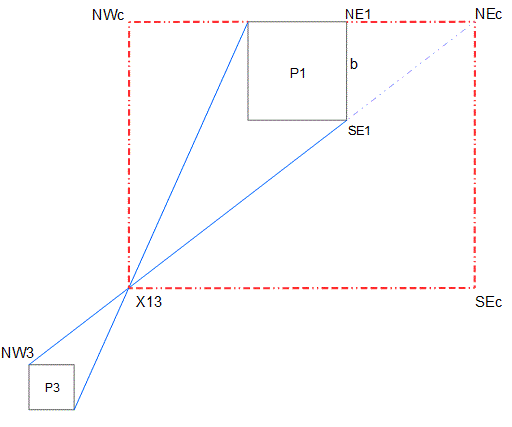
The diagram below shows the three major pyramids of Giza, with two blue lines drawn. P1 is the Great Pyramid, and P2 and P3 are the other two. NW1 is the North West corner of P1, and so on. P2 is dotted and unlabelled.

The two blue lines intersect at the point labelled X13, dividing each of the lines into a long part and a short part. Choose one of the lines, then dividing the whole length of the line by the short part of the line gives 10/pi almost exactly.
I’ve used the average base side lengths Petrie gives for P1 and P3, and also that the east and west sides are oriented to the north, which they very closely are. The result (10/pi) is accurate to less than 0.01 per cent.
In the diagram below I’ve left out P2 and constructed the red rectangle. To do this, I’ve extended the blue line from NW3 to SE1 up to the right (the dotted blue line), and I’ve extended the north base side of P1 to the right such that these extended lines intersect at the point labelled NEc, which stands for North East corner, meaning the north east corner of the dotted red line rectangle. The other corners are labelled similarly except for the south west corner, which is has already been labeled X13, and I don’t want to change it to SWc. It’s an important point.
‘
Some distances calculated are
From X13 to SEc: 31830.97
From SEc to NEc: 24494.55
From NEc to NE1: 11785.02
31830.97 is 10/pi times 10000 almost exactly
24494.55 is Sqrt6 times 10000 almost exactly
11785.02 is 1/(6*sqrt(2)) times 10000 almost exactly
So let’s make these three distances exact in a new diagram. You might as well look at the old diagram because it won’t look any different from a new diagram, that is the red rectangle diagram above. By making these three distances exactly the numbers directly above, where it says ‘almost exactly’, and also making the ratio exactly 10/pi in the blue lines, then the base side of P1, the Great Pyramid, becomes fixed (geometrically) and can be calculated.
Doing this, the base side comes to 9068.9968e. The little ‘e’ means all the digits I could’ve written but didn’t. I write it this way to indicate it’s calculated, not a measurement. The height of P1, to be calculated, depends on the slope angle from the middle of the base side to the apex. Petrie’s range of measurements for that angle (in degrees minutes and seconds) is from 51 49 35 to 51 51 45. This includes arctan(4/pi), which is 51 51 14 Assuming that the angle is indeed arctan(4/pi), the height comes to 5773e, which is exactly the reciprocal of sqrt(3) (times 10000).
The distance between the centres of P1 and P3 now calculates to be 36858.195e. From Petrie’s survey, it’s 36856.6, a difference of just about 1 1/2 inches, different by less than 50 parts per million.
From this we can all realise that there’s an amazing mystery yet to be understood. Why inches?. Why, (and indeed how), the accuracy over such long distances, and who among those people of the past knew about such numbers as sqrt(6) and pi and 11785e. The number 1.1785e occurs quite a few times below – I call it ‘eleven seventy eight’ and I write ‘es8’ as shorthand for it.
I have a lot more amazing things still to come. A lot more. Please read on.
And they’re not tombs.
Second part of section 1
——————————–
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Now for the ‘megalithic yard’
——————————————–
The ‘megalithic yard’ was discovered by professor Alexander Thom from many measurements of stone circles and such like things. His latest estimate for it’s length, in 1978, was 2.720 to 2.724 feet. Pi*sqrt(3)/2 feet is 2.7207 feet, (inside his range), It’s 6*pi*sqrt(3) inches. I use ‘My’ for this unit.
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
The King’s Chamber
——————————
Inside P1 there is the rectangular room known as the King’s Chamber, which I call KC. Petrie gives the dimensions of KC in the survey as (in inches as always)
Length 412.66
Width 206.295
Height 230.9
The length is very close to twice the width. Using pythagoras on the length and width, the diagonal comes to 461.35e, very close to twice the height. 461.35e is 14.13e My, which is close to 10*sqrt(2) My. So, taking the diagonal to be 10*sqrt(2) My, the height to be half that, and the length to be twice the width, then calculating the dimensions gives sqrt(160) sqrt(40) and sqrt(50) in My, which in inches gives
Length = 412.97
Width = 206.49
Height = 230.86
The survey figures for the length and width are averages of measurements at floor level, and the height figure comes from the right hand side of Petrie’s plate 13. There has been some earthquake movement.
More about Alexander Thom at https://rss.onlinelibrary.wiley.com/doi/pdf/10.1111/j.1740-9713.2009.00368.x
The calculated perimeter of P1 is 1111.1 recurring My
P1 Passages and The Main Circle.
————————————————-
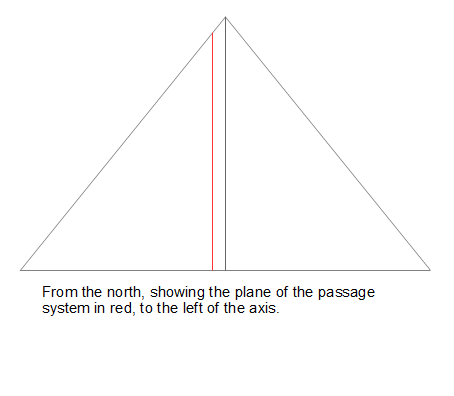
The passages are in a plane parallel to the central North South plane of the Pyramid. The plane is offset about 288 inches to the east, that is, there’s a gap of about 288 inches between the central North South plane and the parallel plane of the passages.
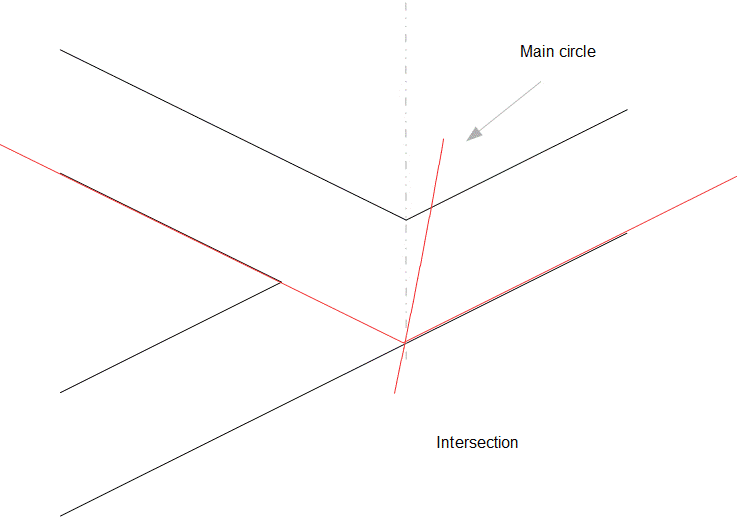
The diagram on the left shows the descending and ascending passages, as they’re called, looking from the east. The descending passage starts fairly low in the north side, and goes below the base level and down through the rock as shown. I’ve drawn the red circle by making it tangential to the sloping sides, and also so that it passes through the intersection of the descending and ascending passages, low down to the right. I call it “The Main Circle”. The diagram on the right shows how “The Main Circle” goes through the intersection of the two passages. You can see that where it crosses the floor of the descending passage, there’s a dotted vertical line up to where the two rooves meet, and a red line up to the left, along the floor of the ascending passage.
The Main Circle has been drawn with a radius of 80 times 1.1785e megalithic yards. That’s 80*es8 My. ^I’ve marked the centre of “The Main Circle” as ‘P’.^
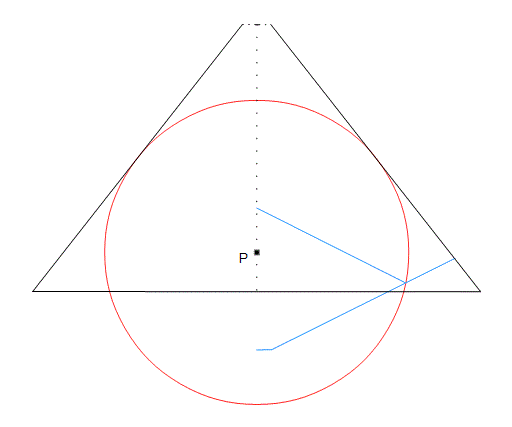
[ The drawings are all made using ODG files and so the red lines are all calculated; these are not rough drawings, they’re accurate. I found the “Main Circle” radius by iterating and examining the output ]
Now draw a circle a quarter the diameter of “The Main Circle” and directly above “The Main Circle”. This circle fits exactly up to the short dotted horizontal line, which is where the passages plane intersects the casing, This is because calculating the ‘offset’ of the passages plane at the top of this circle gives 287.67 rounded, where Petrie gives the offset as 287.0 ± .8, so that 287.67 is within those limits.
The calculation is –
The centre of the main circle is 790.05 inches above the centre of the base at the point P. The radius of the main circle. Now, 80 times 1.1785e My, is 3078e inches, so the height at top of the smaller circle is 790e + 3078e + 3078e/2 which is 5407.227e. Subtracting this from the P1’s height, ( 5773e ), gives 366.275 Multiply this by pi/4 to find the distance from the axis to the outside of the casing at the top of the smaller circle, and it comes to 287.67.
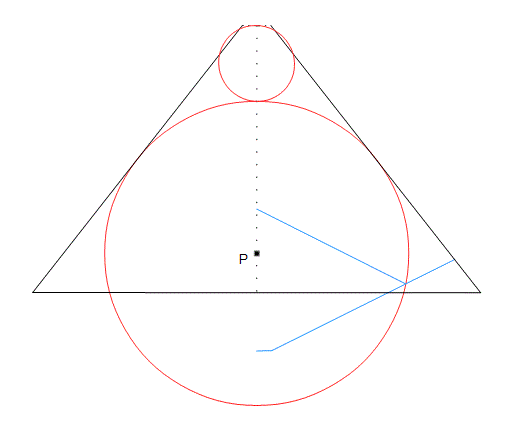
(Some people will see this as the earth and the moon)
100 times 1.178e My is 3847.65 inches. In the KC there’s an empty granite box, which is known as the coffer, or the sarcophagus, and its external width is given by Petrie as 38.5 inches, and you can see that this is 1.178e My, es8 My, that is 1/80 of the radius of the Main circle. There’s more about the coffer later.
Trial Passages
———————
There are some passages cut into the ground a shortish distance somewhere to the east of P1. They are similar to the passages at the intersection of the ascending and descending passages inside P1. Petrie calls them “Trial Passages”, however they suggest the presence of the upper passages of P1 before those upper passages were discovered. The builders had concealed the ascending passage, and thus the grand gallery and the other upper rooms couldn’t be casually found. They weren’t found until the year 831 by the Caliph Al Mamun breaking in.
The trial passages can be seen on Petrie Plate 3b. ( http://www.ronaldbirdsall.com/gizeh/ click on the left of the blue line)
Petrie doesn’t say where they are, but at http://www.ancient-wisdom.com/Ghizaarchitecture.htm#2.55 it says
“They lie 87.50 m. from the eastern base of Khufu’s pyramid (the Great Pyramid, P1) and 43.50 m. north of the east-west axis.”
Using pythagoras on these two lengths gives 97.716 metres which is 117.83+ My – a familiar number now, eleven seventy eight.
(Looks like it might be a ratio of 2:1 for the sides of the triangle).
Petrie’s drawing labelled “plan of passage mouth” shows three measurements across the front, that’s in the small diagram to the left (on Plate 3b). They are 18.7 inches, 41.33 inches, and 19.8 inches.
The two side measurements, 18.7 and 19.8, add to 38.5 where 38.476e inches is 1.178e My, eleven seventy eight again.
The three together add to 79.83 inches, which is 2.445 My. If the number is meant to be sqrt(6), then the width would be 79.97e inches.
sqrt(6) – es8 gives a difference of 1.27e My which is 41.5 inches rounded, corresponding with the measurement of 41.33 inches, a big difference although less than half one percent. Petrie’s measurements of the Pyramid passage widths is 41.53 inches with a mean difference of .07 inches.
The Queen’s Chamber (QC)
————————
Quoting Petrie, “184.47 is the top of the N. and S. walls, and a joint on the E. and W. walls. 179.09 is a joint that occurs at each side of the E. and W. walls, but which does not run far, being soon shifted upward to the 184 level.”
Including 179.09 as what might be a significant joint height, and with the width and length and the height of the roof ridge being given as below, this further surprise occurs
10/CubeRoot(3) My is 226.37 inches where Petrie gives 227.50, for the length
10/CubeRoot(4) My is 205.67 inches where Petrie gives 205.67, for the width
10/CubeRoot(6) My is 179.67 inches where Petrie gives 179.09, for the joint
and
10/CubeRoot(2.357e) My is 245.32 inches where Petrie gives 245.1, for the ridge height. 2.357e is twice eleven seventy eight (1.1785e)

I include this rough diagram to emphasise that the ridge height uses 2*es8. I don’t think the Builders built this room just for this reason, that is to bring attention to cube roots, even special ones, there’s also the QC’s enigmatic ‘niche’. (later).
————————————-
The descending and ascending passages
[20191112] Now I have some suggestions about the main two internal passages in P1, the descending passage and the ascending passage. I’ve done quite a few calculations, and while the diameter of what I call the intermediate red circle below might be a better one than another, it’s still arbitrary. There’s a better reason for choosing the angle between them (the passages). And now, [20191210], further down, just below the next bit, I’ve found what I think could be the best one, but please read on. The origin for coordinates is at the middle of the base of the passages plane.
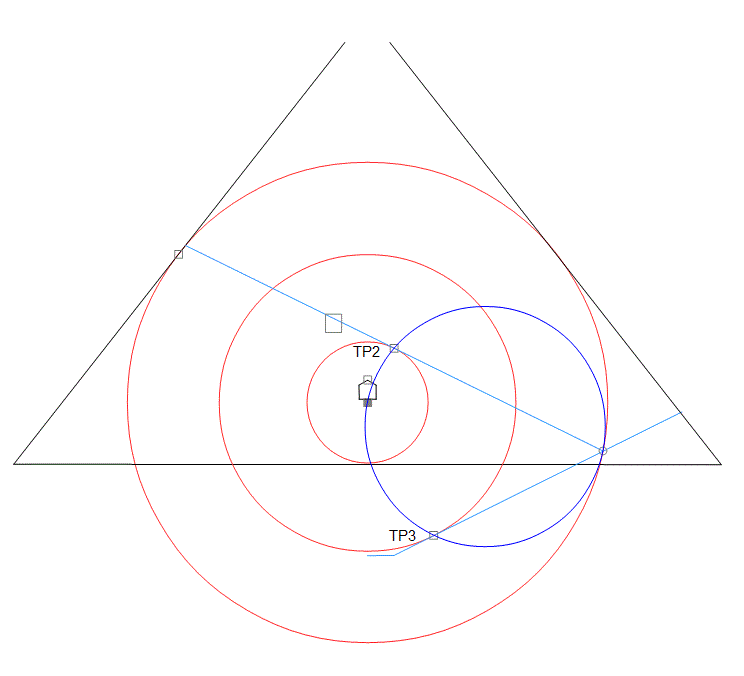
I’ve chosen the intermediate red circle to have a radius of 3078e – 1178e inches. (1899.608e inches) . I then found the tangent point TP3 using the angle Petrie gives for the descending passage. The x coordinate was 848,285+ which is very close to 848.528+ (that’s 6*sqrt(2) the reciprocal of es8). So I chose the x coordinate to be exactly 6*sqrt(2) making the angle slightly bigger than Petrie’s angle, and calculated the intersection point of the descending passage and the Main circle.
The angle between the two passages according to Petrie’s values, is 53.74 degrees. I’m going to use the number ‘a quarter of 10/pi’ and find the arcsin of this number, which is 52.728+ degrees. The reason for choosing this angle is towards the end of Section 2. So subtracting this angle from the descending passage angle gives an ascending passage angle, Then find the tangent point TP2, (and the radius of the small red circle). Because of choosing this angle, the distance TP2 to TP3 is exactly sqrt(6). This will always be so, no matter where the intersection is, (on the main circle), no matter which tangent point you calculate first, or no matter what the size of the first circle you choose is (that is, either the intermediate or the inner circle), It’s because of the chosen angle of arcsin(quarter 10/pi) only. Then draw the blue circle. The blue circle is half the radius of the Main circle, All this shows a relationship between 10/pi (from the angle difference), sqrt(6), from the distance TP2 to TP3, and es8 from the blue circle, say, or the Main circle, just as in the red rectangle (and also the blue lines) at the beginning. Below is a diagram of the passages according to the measurements Petrie gives, with the red lines showing the results of the calculations. The calculated descending angle is 26 31 52.5 The red arc is an arc of the “main circle”, and goes through the roof where there might be a vertical passage, possibly indicated by the ‘trial’ passages.

But the radius (1899.608e) reminded me of 1901e which, in the diagram below, is the height of the main circle tangent point TP1 above P, that is the vertical green line from TP1 to C. I made the intermedate circle radius this number..
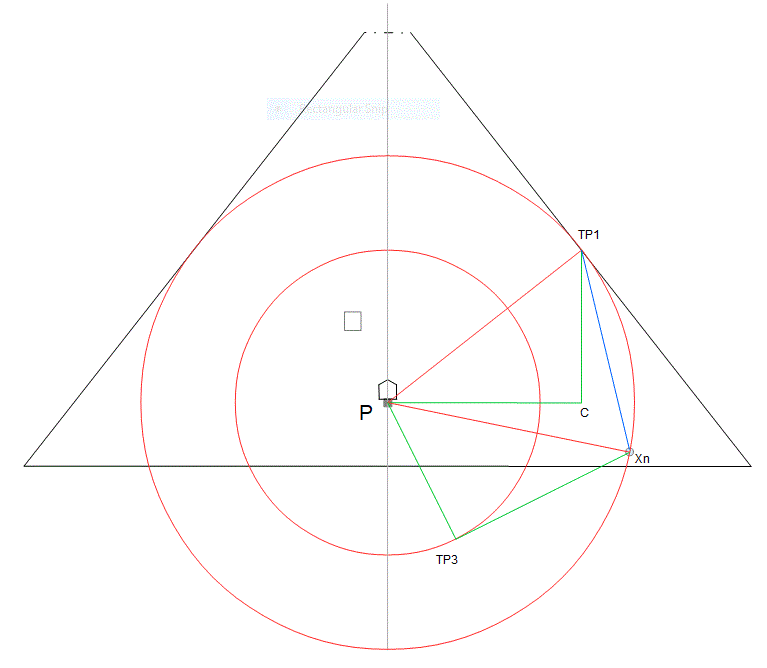
The triangle P TP1 C is the same as the triangle P Xn TP3 except it’s flipped over. The line P TP3 corresponds to the line TP1 C. I had noticed that the angle C TP1 Xn between the blue line and the vertical green line might be about 13 degrees or so. The slope of the blue line came to -4.24e so I took it to be -3*sqrt(2), and choosing it to be that number gave 13.26e degrees for the angle. Double this (for symmetry about the vertical say) is 26.525e degrees which is 26 31 31+ where Petrie’s angle is 26 31 23 Subtracting arcsin(quarter of 10/pi) from this gives the ascending angle of -26 12 11.3 where Petrie’s angle is -26 12 50
The position of TP3 was calculated using the new angle (26.525e) from the intersection, and the radius of the intermediate circle created is equal to the height C to TP1. (- slight wobble in the fifteenth digit, although it looks like it must be exact by geometry (hard to prove?)).
TP2 (not shown) to TP3 will still be sqrt(6). This looks like the best idea so far, especially considering the green triangles, and the angle, arcsin(3*sqrt(2).
The intersection point is at 3015.03 170.02 The distance from the intersection point to the entrance is 1110.34, close to Petrie’s value of 1110.64, and well within his limits. Calculating the intersection point on the casing near the entrance, now gives a height of 666.97. The top of the 18th course averages 666.95 .
Petrie gives 668.2 ± .1 and 524.1 ± .3 inward, (The above gives the 666.97 and inward 523.84 from the base). These two coordinates are outside Petrie’s range, but only different by less than 0.2% All other calculations everywhere else are within his ranges.
In ‘Correction to Section 64 Summary Table’ Ronald Birdsall says the following.
In section 36, two angles are presented for T: 26º 31′ 23″ and 26º 26′ 42″
Calculating the elevation h for each of these angles yields 172.2 and 173.6, respectively. Neither of these values are 179.9 or 172.9. But taking the average of the two angles (as was Petrie’s habit when faced with multiple values for the same measurement) yields an elevation of 172.9
Some more about the KC and the QC
————————————————
[20181115]
50*es8 My is 1923.82e inches and this is the ceiling height, above base level, of the KC roof, and is within Petrie’s measurements, (1921.6 to 1923.7 ± .6 above pavement), very close to the upper limit. (1924.3)
Subtracting the floor to ceiling distance, which is sqrt(50) My, gives 1692.96e for the height of the floor above base level. This is 44*es8, and is within Petrie’s limits (1691.4 to 1693.7 ± .6 above pavement).
The level Petrie gives above base for the ridge, the peaked roof of the QC, is 1078.7. The point P, the centre of the main circle, is at the level above base 790.048e. The difference is about 288.65, which is very close to half of 577.3e where 5773e is the height of P1. Adding 288.6e to the level at P of 790.048e gives 1078.72e.
Petrie gives the distance from the centre line to the north wall at base of the KC as 330.6 ± .8 and adding half the KC width, 103.2e, to this gives 433.8, where sqrt(3)/4 is 433.0e. 433.0e would only just squeeze inside the limit.
Please write to me at [email protected] – Please put ‘Es8’ at the beginning of the Subject line.
ISince the first version in November 2015, only one person (apart from family) has written to me, (who said “the Egyptians used cubits”, so I was wrong). Please drop me a remark or two.

It’ll be easier not to read the description, (or explanation), that is, the next paragraph, you can just go to the comparisons below it.
The external width was found (by Petrie) by adding the measured thickness of each side and the measured internal width; the numbers are 5.87 26.81 and 5.82, and it can be seen that the thicknesses add to 11.69. If the thicknesses were meant to add to 11.785e inches, and the external width is taken as 1.1785e My, then the internal width would be given by 1.1785e My – 11.785e inches, which comes to 26.69+ inches compared with 26.81. Considering the external length, 2.357e My is 76.95+ inches and adding 11.78e to this gives 88.74+, not far off Petrie’s external length of 89.62 (just under one percent). So, the lengths and widths might have been meant to be
External width es8 My = 38.48 inches —– Petrie 38.50
Internal width es8 My – 10*es8 inches = 38.48 – 11.79 = 26.69 inches —– Petrie 26.81
External length 2es8 My + 10*es8 inches = 76.95 + 11.79 = 88.74 inches —– Petrie 89.62
Internal length 2es8 My 76.95 inches —– Petrie 78.06
The last figure is out by nearly 1.5 percent, which is imprecise compared with other measurements up to now.
The coffer measurements are the averages of measurements made from what seems like a best fit of planes, and Petrie gives variations from those planes in tables of variations. The variations in the lengths can be up to two (or even three) tenths of an inch here and there, so that it could be that the above were the design lengths and widths. Maybe the coffer was difficult to make. He points out in section 57 of the survey that there were a few mistakes in its making, cutting it in the wrong place and then trying again, and some other things, and by the way, there’s no reason to assume that it was made at the same time as any other particular part of the whole Giza area. One can speculate.
The external height, from Petrie, is 41.31 inches. This is very close to 6 times the measured thickness of the base, and is very close to one tenth of the length of the KC itself, the chamber that contains it. So taking it as that, as (Root160)/10 My, and making the thickness of the base a sixth of that, we have the below.
External height 41.297 inches —– Petrie 41.31
Base 6.883 inches —– Petrie 6.89
Inner depth 34.414 —– Petrie 34.42
Possibly the unit of some multiple of es8 My being used for the Main Circle and so on is 1.1785e My, being the external width of the granite box. Taking the external width of the box as the unit, then the radius of the main circle is 80 of these, the KC roof level is 50 of these, and the KC floor level is 44 of these.
41.33 inches is also the middle measure at the trial passage mouth.
————————————————
The 35th Course
P1 appears to have been built of over 203 layers, or courses, of stones, and apart from the bottom two, the 35th is the thickest. The level of the bottom of this course is at a bit over 1137 inches, and the top at about 1187 inches (above the base), so that about 80% up is the level es8 1178.5e
————————————————
Height of P2
Petrie gives height as 5,664 ± 13 inches, that’s a range of 5651 to 5677 which includes 4*sqrt(2) (times 1000) inches, which is 5656.85e. It also includes sqrt(3) (times 100) My, which is 5654.86e inches. Both of these are near the lower limit, the limits being 5651 and 5677. I prefer the 4*sqrt(2) number, the 5656.85e inches, which is 471.4e feet, a more recognisable number, being 4 times es8. I don’t like talking in feet; just now I think feet were invented later. I can’t see why the base is what it is. Petrie gives a mean of 8474.9 inches, which is 706.24 feet, close to 1/sqrt(2) (times 1000) feet, but nevertheless nearly a foot different. Maybe P2 was built later. Certainly its clumsier looking stonework suggests that.
————————————————
Height of P3
Petrie gives for the height h3 of P3 as 2564 ± 15 or 2580.8 ± 2 He’s given these two widely different measurements for h3 using two different ways of measuring it. He says, (about the angle of the side), quote, “the best conclusion seems to be 51º 0′ ± 10′. But from a consideration of the granite courses (see below), the angle would be 51º 10′ 30″ ± 1′ 20” unquote. Using the “best conclusion” for the angle, and using the calculated base length of 4154.185+ from above, (the blue lines at the beginning), then the height h3 is 4154.185+ * tan(51) = 2564.99+, so h3 might be pi/4 My, (times 100), which is 2564.198e inches. Starting with pi/4 My, the angle will be 50.99+ degrees. Not interestingly different from 51 degrees, so it looks like his “best conclusion” was spot on, despite the difficulties. With this, and the measurements which gave rise to the broken red line “corners” rectangle, (just after the blue lines at the beginning), you might conclude that the accuracy of the entire survey is similarly impressive. That’s generalising from the particular.
The red granite casing on the lower part goes about a quarter of the way up, and its measured height is 645.2 (± .5 (?)) inches. Petrie multiplies this by four to produce the second estimate,.
Section 2
The megalithic yard was originally discovered by Professsor Alexander Thom during extensive measuring of stone circles and so on in the British Isles, giving 2.722 ± 0.002 feet, although it hasn’t been accepted by everybody as a true ancient measuring unit. Pi*sqrt(3)/2 is 2.7206e which is within his limits. I prefer to use it as 6*pi*sqrt(3) inches. I use ‘My’ for this unit. Now, there’s another one, that is another number like 6*pi*sqrt(3), or number string say, which I found from the following. Not far from the huge Avebury stone circle in England there’s another smaller circle which hasn’t been dug up, but you can see it [no longer] on touchmap at latlon 51.420108 -1.830913, and in these pictures. [It can no longer be seen on iTouchmap]. I call it Found_Circle. Found_Circle is at the bottom right of the wide view below. You can just see it at the bottom right corner. (I’ll zoom in).

Zooming in a bit. [20180809] You can no longer see it on TouchMap or Google maps.

Here it is close up.

And now with markers.

The diameter of the circle of markers is 117.85e My. This number looks like sqrt(2)/12 which is 0.11785e, so the diameter is sqrt(2)/12 (times 1000) My, and a circle of diameter four times this, of 471.4e My, fits quite well on the Avebury Circle below.

Below I’ve shown a lone blue marker near the centre of the Avebury circle. The distance from this marker to the centre of Found_Circle is 1.1785e miles, – and also, the distance from the marker to the centre of Stonehenge, way to the south, is 17.32e miles. This is sqrt(3) (times 10) miles.

For the distances I’ve assumed the earth is a sphere of radius 3960 miles, and maybe the Builders have too. The same string of digits is used for the diameter of Found_Circle in megalithic yards and its distance in miles from the Avebury circle. That is 11785e. (I call this string of digits ‘es8’ for ‘eleven seventy eight’, so that ‘es8’ will mean this string irrespective of where the decimal point is). The circle of markers at the Avebury circle have a radius which is double this, using the string 2357e (being 235.7e My). 51.428675 -1.853878 (All the lats and lons given are from getlatlon.net and the circles come from MapDev)
Below here are what I think must be all the rest of the large stone circles in Britain with their surprising dimensions, followed by some small ones, or their descriptions, but first, ‘The Sanctury’. I’ve placed the red circles on the stone sockets and post holes in this one, and over the stone circles in the rest, sometimes obscuring them, as in the ‘Devil’s quoits, next after the Sanctuary.
‘The Sanctury’ Inner radius 23.57 feet, Outer radius 23.57 My ! 51.411109 -1.831301
‘The Devil’s Quoits’ – Inner radius 23.57 My, Outer radius 47.14 My.
There are only a few stones left in it’s outer circle, up to the top right, that is the north east. 47.14 My is the radius of the circle drawn. The inner circle is the same size as the outer circle of the Sanctuary. 51.740016 -1.405865
‘Swinside Stone Circle’ Radius 47.14 feet (4es8) 54.282477 -3.273850

‘Rollright Stones’ radius 612e inches (diameter sqrt(6)/2) 51.97552 -1.570806
‘The Hurlers’ (Northern one of three)’ radius 20.41 My (es8*sqrt(3)) 50.516319 -4.458215
The Ring of Brodgar and the southern inner circle of Avebury both seemed at first to be same size as Found_circle, but this is not so. The Ring of Brodgar on the left has a radius of 2041 (es8*sqrt(3)) inches, The southern inner circle of Avebury is on the right, of diameter 117.85 My, same as Found_Circle. 59.001471 -3.229691
[20200813]

‘Stanton Drew’ diameter pi*sqrt(2) inches (half on the left, half on the right) 51.367115 -2.576065
‘Beltany’ diameter 1732 inches (sqrt(3)) 54.850364 -7.604797
‘Castlerigg’ diameter 1178 inches 54.602840 -3.098401


‘Girdle Stanes’ radius 23.57 My 55.253864 -3.176041
The merry maidens 38.48 feet, 12 times the width of the granite box in the KC 50.065123 -5.588728
Back to the Hurlers, not far above, where I show the northern one of the three. The centre of the middle one is at about 50.516320 -4.458208. The southern one doesn’t really have quite enough stones remaining, but it does seem that it could’ve been the same size as the northern one. The middle one might’ve been the same as the others times a quarter of 10/pi
And there’s this one in Syria, hard to make anything out, but the circle drawn is the same as the Main Circle and the Heelstone circle (see below), with radius 3078 inches. Wikpedia has a good picture of it, and says it’s 520 feet diameter and then (160 m) which is 525 feet, anyway the 3078 inches could be inside outside or probably somewhere in the middle of the outer ring, and the inner rings look like even divisions at Wikipedia. Intentional ? It’s not quite a circle anyway.
There are some more – Torhouse 10.2 My possibly – ‘Cairnpapple’ don’t know – ‘Sunhoney’ 10.2 My possibly but not enough stones visible – ‘Scorhill’ radius 47.14 feet but a bit broken – ‘Tregeseal East’, it looks like it’s an ellipse – There are many others, too small or too fuzzy or too hard to find.
The outlying stone at Long Meg is 235.7 feet from a point possibly at the centre of the ‘ring’ 54.728047 -2.667495 , 54.727598 -2.668287 – the Adam and Eve stones are 47.14 feet apart. 51.422813 -1.873281
Very near the Ring of Brodgar in the Orkney Islands are the Stones of Stenness, and the chambered cairn of Maes Howe. The distance from Maes Howe to the Stennes Stones as 3847.65 feet, that’s between the two white dots below with the rec arcs through them, ( 38.47e inches is the width of the granite box in the KC ) 58.9966 -3.1882 -58.994043 -3.208051
That’s Stenness Stones in the middle, and Maes Howe on the right. The little white dots are the centres of the two red circles on the left,

Stonehenge has a circular ditch frequently said to be about 320 feet in diameter where es8 My is 320.64 feet. The distance from the stonehenge centre to the heel stone is 80*es8 My, 3078e inches, the same as the radius of “The Main Circle” of P1. The angle round from the centre to the heelstone from the north south line is the pi angle, so the heelstone corresponds to the northern tangent point of “The Main Circle” at TP1 in the P1 diagrams.

Radius 3078e inches
Inner radius 40.82 feet (2*es8*sqrt(3)) Outer radius (sarsen circle) 20.41 that’s My sqrt(3)*es8
———————————————
[20180809] Below is a circle centred on Found_Circle, with the radius 1.1785e miles. It goes through the Avebury circle at the single marker in the picture of Avebury way above, and also through Silbury Hill lower down on the left, about through the centre, (Also, it cuts the West Kennet long barrow about in half).
Found_circle’s diameter is es8 My, and the distance of Found_circle from both Silbury Hill and Avebury is es8 miles. Es8 My is the outer width of the coffer.
[20181016] Later I thought I’d calculate the sides and angles for the triangle from Found_Circle (call it FC) to the single intersection point in Avebury (the lone blue marker way above) (call it AVX) and the approximate centre of Silbury_Hill (call it SH). The angle FC AVX SH was 1.176+ radians (very nearly es8 radians 1.1785e) and the angle AVX FC SH was 0.7959+ radians, (very nearly a quarter of 10/pi). I made both of these angles exact, and calculated a new position for SH, which turns out to be in the middle of the flat bit on the top. See pic below.

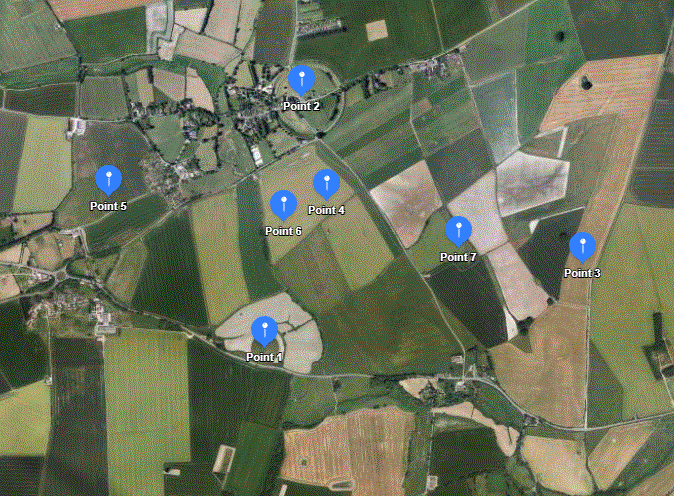
)[20181115] I was looking at the map around here a bit later, and I caught sight of a crop circle which was new on 22 Apr 2017.
You can see it at https://www.youtube.com/watch ?v=A5OBC_TstYU or search for ‘waden hill crop circle’ and scroll down through images.t’s at point2 below. (Point 4 is the lone marker at Avebury, and Point 3 is at Silbury Hill). It looked like a nice curve from AVX through the crop circle CC, to SH, so I calculated the centre for these three points, and found it was very close to pi/4 miles from each of AVX and SH. I calculated the points pi/4 miles from AVX and SH, the western one is at point1 in the picture below, and using that for a centre, calculated points through the crop circle and chose the one labelled point2, very close to its centre. The left picture thus shows three points on a circle of radius pi/4 miles. AVX SH and CC.
On the right there’s a closeup of point 2. The little upward pointing line from point2 points towards the centre of the Avebury ring.
[20190204] You can no longer see CC on iTouchMap and Google maps.
In the picture below, point6 is at the intersection of AVX to SH and Point5 to FC (at Point3). The angles there aren’t right angles, but they’re very close.
—-
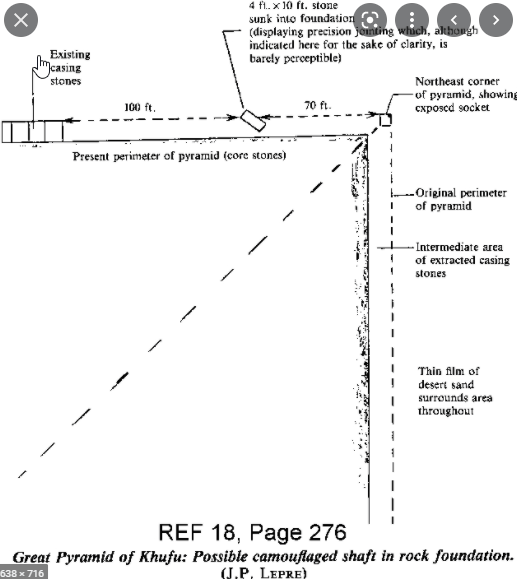
And now for the Oblique Stone
From J P Lepre
18:276] – “About 70 feet along the north side of the Great Pyramid from the northeast corner is a 4×10 ft stone sunk into the foundation at an angle. The joints are very precise and this is the only stone in the foundation perimeter not at a right angle to normal construction. It would have been covered by the mantle but is now accessible since the mantle is gone. It is very likely an entrance.“
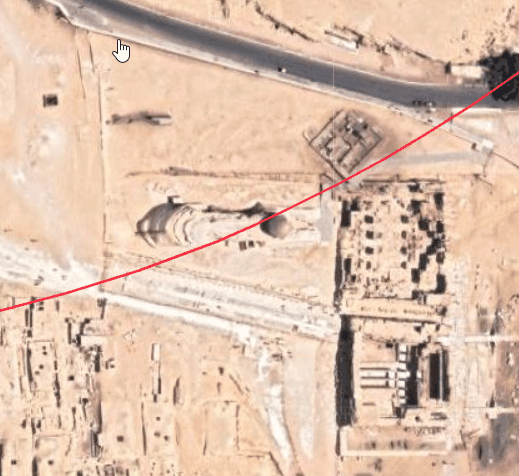
In his diagram (below left), at the top, it says ‘4 ft by 10 ft stone’ pointing to the oblique stone. It shows part of the stone sticking a bit beyond the edge where the casing stones were, showing that it wasn’t entirely covered. You can see some of the remaining few casing stones to the left. The diagram on the right shows the points OS (oblique stone), mW1 (mid west P1), mE1 (mid east P1) and TP (trial passages).
mE1 to TP is is about 117.8 My, or some point on or near the trial passages, from the trial passages paragraph way above. OS to TP is about 100*pi/2 My, by measuring. OS to mE1 is about 100*sqrt(2) My, by measuring, and OS to mW1 is about 287.67e My, where the passage offset is 287.67e in inches, and as I said at the time I first wrote about the oblique stone “a rather odd coincidence, if it is one”.

r[20210824] Years after first writing about the oblique stone, I thought to see if it really is a “rather odd coincidence” about the distance mW1 to OS (oblique stone), and could the position of TP (trial passages) be calculated. So, using the distances as exact.
Points mW1 and mE1 give the coordinates for OS of 3687.94 4538.91, just 4.4 inches outside the casing , and about 846.6 iinches from the North East (70.55 feet), at latlon 29.980196 31.135148
then points OS and mE1 give the coordinates for TP of 7974.49 1723.61 at latlon 29.979554 31.136278
You can put the lat and lon into google maps and zoom in. The rectangle to the south of the red marker is the entrance to the trial passages, and the hazy shadowy square to the north must be where the northern exit is. If you google for ‘trial passages position’ (not in quotes) you’ll be able to see that the calculated red marker is close to being above the intersection. It looks to be just over the east wall of the intersection.
TP is west from mE1 by 3440.00 and north by 1723.61 not a ratio of 2 to 1, (very nearly, but not)
I haven’t been able to find anything about this stone from anywhere other than places originating from him ( J P Lepre )
I wondered if this stone may relate to any other points in the area. and it does. From the point OS as centre, a circle of radius 23570e inches arcs through the sphinx as shown below on the left.
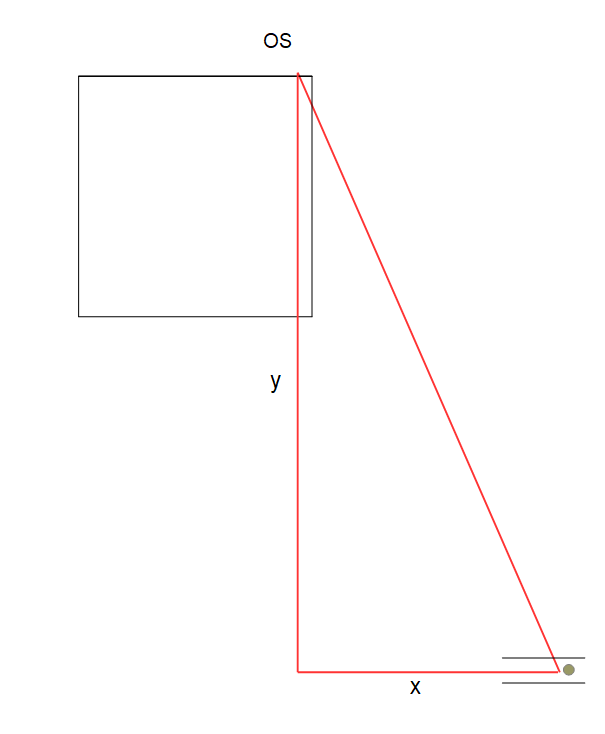
I chose a spot on the red arc a little behind the head, more or less half way between the sphynx’s sides. In the right hand diagram, the small grey circle is the head, and the two small parallel lines are the sides. I then drew the red triangle (OS is the oblique stone), and calculated the lengths of its sides, that’s the lengths of the lines y and x. The ratio y/x was close to 4/pi + 1, that’s about 2.27 So making these two lengths have the exact ratio 4/pi + 1 and keeping the length of the hypotenuse as 23570e, the result for the coordinates of the (somewhat dulled) red marker in the next picture are 13178.78e -17036.06e (latlon 29.975270 31.137650 )

[20181016]
I found the number es8 a long time before I drew the blue lines and the red rectangle on the Giza layout at the beginning of section one, and it was a great surprise to see 11785 inches appear in the red rectangle, (from NE1 to NEc).
It was about two years after making this webpage that I was prompted to extend the blue lines in the other direction (not spotting anything). And of course you can draw similar lines using P2, or anything else, and say that it’s only a coincidence about the particular diagram I’ve used, but then it all depends whether you think there’s a design or not.
First version 2015-11-15
then 2018-05-30
then 2019-12-11
then 2020-08-13
then 2020-07-29
then 2021-08-26
with minor changes from time to time
_________________________________________________________________________________ _________________________________________________________________________________| _________________________________________________________________________________|
Some of this section is worthy of being completely ignored, but perhaps not all of it. Most of the things below are less believable, and/or more speculative, and/or less convincing. Please allow that the discoveries above have been made by looking for impossible things, and that’s why I’m doing the same thing below. There may be some clues.
Anyway, please read “The Last Thing”
_________________________________________________________________________________ _________________________________________________________________________________| _________________________________________________________________________________ _________________________________________________________________________________|
The niche in the QC and more about the QC walls.
————————————————————————————————
In the QC the width the length and the ridge height and one of the joint heights conformed with 10/CubeRoot(x).
x = 10*sqrt(2)/4 My is 214.31 inches which corresponds with the first joint below the ridge at 214.35
x = 100*sqrt(2)/4 My is 99.47 inches which corresponds with the sixth joint below the ridge at 99.13 ?
x = 10*sqrt(5)/4 My is 183.96 inches which corresponds with the second joint below the ridge at 184.47 maybe, but it’s a bit far off, and there aren’t any other appearances of sqrt(5) that I’ve seen anywhere, so it’s maybe more likely 4*sqrt(2) My if anything, which is 184.69 inches,
The height of the ridge is 183.8 which looks like h/pi/10 at 183.8 , but it also might be that it’s the solution to 1/CubeRoot(x) = x which gives 5.62e My, which is 183.6 , only 0.2 of an inch away
183.8 is also the distance from the centre of the base of the passage system (the origin) to (Petrie) “the absolute place of the floor end at the latitude of the E. wall of the gallery” i.e. the beginning of the Grand Gallery 1836.7, using co-ordinates 1626.8 ± .8 and 852.6 from (Petrie 1626.8 ± .8 and 852.6 ± 3). Using 1626.8 for the x value on the ascending passage gives 853.2 for the y value, within the limits.
It’s possibly the length of the roof of the Grand Gallery. Quoting from Petrie “From this the length of the roof of the gallery is 1688.9 – 40.45 = 1648.4 horizontal, or 1838.6 sloping”
It could be the horizontal distance from centre line of the QC to the upward bend of the South air shaft, 183.2, Petrie giving the rough figure of 80 inches from the wall to the bend. (On the other hand, If the 80 inches is sqrt(6) My, then the distance is 182.8e)
The niche is in the east wall of the QC. At the top, its centre is offset from the centre of the east wall by (Petrie) 25.08 inches, and the top is (Petrie) 183.8 inches above the floor. To find the offset, divide 1.1785e My by 2 to give 0.5892e, and take the square root of this. It’s 0.7676+ My which is 25.06+ inches. The next three lines describe the short list below them. To find the width at the top, take the value of the offset at the top, that’s 0.7676e My, and multiply by pi/4, giving 0.603 My which is 19.68 inches where Petrie gives 19.75 To find the width at the bottom, take the width at the top, that’s 0.603 My and multiply by pi, giving 1.894 My which is 61.84 inches where Petrie gives 61.44 To find the depth of the niche take the square root of pi/2 giving 1.25 My giving 40.92 inches where Petrie gives 40.72 for the depth at the top. [Now, 20200820, 40.82 fits better, 2*sqrt(3)*es8, but I’ll leave the old stuff here]. So,
height: h/pi inches
offset: sqrt(es8/2) My 0.77 My = 25.06 inches , Petrie 25.08
top: offset*pi/4 My 0.61 My = 19.68 inches , Petrie 19.75
bottom: top*pi My 1.89 My = 61.84 inches , Petrie 61.44
depth: sqrt(pi/2) My 1.25 My = 40.92 inches , Petrie 40.72 (see 40.82 in the square brackets just above)
Both the offset and the depth vary going from the top to the floor. Also the width of the bottom seems to be too small for the above idea, by 4 tenths of an inch, which is quite a bit compared with the accuracy in section 1. Also the depth is 0.2 inches different. The ratio of Petrie’s top to bottom is 3.11 which is quite a long way from pi. 41 inches occurs somewhere in the measurements of the widths and/or heights of the ascending and descending passages I think, and for the thickness of the base of the coffer at 41.3 inches. I did say in my first version that there were some *speculative* things to say about the QC. but what’s it for, the niche ? I wonder, from the things that were found in the QC northern air shaft, that it might have held a pendulum. See http://www.theglobaleducationproject.org/egypt/studyguide/gpinterior.php for pictures of the sphere and the hook thing, and the handle thing (at the bottom). I think the leading thing about the above is that the height of the niche is 183.8 inches (especially considering this string occurs elsewhere at least twice). I considered that the width might be widening by parts of es8 going down, and while this looks to be possible, it looks far too speculative. Or wrong.
————————————————
Lines towards P2
————————————–
X12 is the point of intersection of lines from P1 and P2 the same way as X13 is the point of intersection of lines from P1 and P3 shown earlier. Similarly X23 is found.
It might be an idea to look at the diagram below before reading the description.
In the diagram there are two red lines drawn from the trial passages point TP, where the two red lines meet at the top right, and there are two unlabelled arrows. The top red line, through X12, intersects the NW1,SE3 line very close to the north baseline of P2, where the top unlabelled arrow points. The bottom red line, through X23, intersects the SE1,NW3 line very close to the south baseline of P2, where the bottom unlabelled arrow points.

The southern unlabelled point is 3.37 inches south from the south baseline of P2, and the northern unlabelled point is 20.12 inches north of the north baseline. Although 20+ inches is not much considering the scale of the layout, it’s still big enough to be notable compared with everything else. The two distances add to 23.49, very close to 23.57e, but this doesn’t look significant. You can move P2 to thousands of points within an inch of where it is, and make the distance 23.57e. I call the number HighLow.
“Zem and the art of herding pigs, and the mystery of the strange fruit.”

Green circle
I’ve squeezed the blue circle from section 1 up into the peak and drawn the green circle through TP3 P and TP5. The reddish line intersects the descending passage at exactly the same co-ordinates as the green circle intersects the descending passage. The point is up and away from the scored lines at floor level by about 18 inches, and might be on what some writers have thought to be a significant joint (one of two). Neatly, the green line going up from point P and through TP5 is parallel to the south side line.
The Air Shafts
I’ve done some iterating varying many measurements between their extremes without finding anything that I could relate to anything much. The points where any and all of the airshafts intersect shift around markedly, especially when varying the shaft angles within their (Petrie’s) extremes. Not all of them go straight anyway. Rudolf Gantenbrink made some measurements with his very cool crawling robot during the time when he famously discovered the secret door at the end of the QC southern air shaft. Anyhow: The floor of the KC’s northern air shaft appears to exit at height pi inches (times 1000). Just doing the QC south channel, the length of the horizontal part before the upward bend is given as 80 inches where sqrt(6) My is 79.97 inches – Petrie says quote “67.44 is a joint level, signalized by the top of the doorway and of the channel mouths in N. and S. walls.” unquote. 67.44″ is 2.066 rounded My. This number is about (4/pi)^3 which is 2.064e. 2.064e My is 67.39 inches. Please remember that the heading of this section suggests ignoring some of it. From pictures it looks like this lines up with the lowest ledge of the niche. Petrie gives 67.14 for this. The length of the horizontal beginning part QC north channel is 76 inches, which I can’t do anything with. I can’t make anything of the scored lines. I’ve done hardly anything about the Grand Gallery.
————————————————
1/sqrt(3) minus 1/sqrt(6), (which is equal to h1 – h1/sqrt(2) is 1691.02. Petrie gives 1692.8 ± .6 for “the step” near the end of the Grand Gallery. About 1/2 this is some level in or near the QC, or at its entrance. This is not a new idea.
[20190204] But it’s probably wrong. Much more likely it’s 44 times es8 My, that’s 1692.96+ , which is within range (see section 1, KC roof 50 floor 44).
————————————————
It looks like a circle of radius 2357e inches centred perhaps on the axis somewhere near the level of the centre of KC or its lower part might go through the grotto and/or through or near the ends of the QC air channels, or at least the southern one, not quite knowing where the northern one ends. Thanks to Clive Ross for the idea of this circle, and also very much for the idea of “The Main Circle”.
————————————————
Some Cursuses
The stonehenge cursus is sqrt(3) miles long (one tenth of the Avebury Stonehenge distance) by calculation from the lat and lon for the end markers.


Cursus_W_Terminus 51.185316 -1.844853 Cursus_E_Terminus 51.187785 -1.805065 I seem to remember somewhere that it goes, or once did go into the trees there, where the marker is. The lesser stonehenge cursus is pi/2 times 10000 inches long. The Dorset cursus, which is the longest cursus, is 11785e My long I don’t know how many cursuses there are, but there seem to be a fair few. The Springfield cursus 700 metres doesn’t seem to be anything – other sites say it’s 670 metres see [20200820 no longer there] http://www.archaeologyuk.org/ba/ba69/feat1.shtml which gives the approximate lengths of the lesser cursus and the Dorset cursus. “… the 400 metre-long Stonehenge Lesser Cursus …” – 10000*pi/2 inches is 398.98+ metres “The longest, the Dorset Cursus near Blandford, is about six miles long (9.75km) …” — 11785e My is 9.77+ km or 6.07+ miles
————————————————
Silbury Hill
Wikipedia in the second paragraph title Structure says for Silbury Hill – 30 metres diameter for the flat top, 40 metres for the height, and 167 metres for the diameter at the base — 30 metres is 1181.1 inches, so starting with 1178.5e inches it’s 29.934 metres. 40 metres is 1574.8 inches, so starting with 1570.796+ inches, that’s pi/2 inches, it’s 39.898- metres. 167 metres is 6574.80 inches. I can’t make anything out of this, except that sqrt(3)*es8 is 169.27 metres, more than 1 percent out, and a bit fanciful anyway.
————————————————
Teotihuacan
at http://latino.foxnews.com/latino/entertainment/2011/10/27/scientist-finds-numerical-pattern-in-ancient-mexican-city/ it said (gone now) ” … Saburo Sugiyama discovered … Teotihuacán … numerical measure … 83 centimeters “: (1 My is 82.93 cm). He says the base of the big pyramid is 260 times 83 cm and the base of the small pyramid is 105 times 83 cm and he adds these to get 365, being the number of days in a year.
However, 260*83 cm = 21580 cm, which is 8496.06 inches. This is fairly close to 8485e inches, so it may be that the base of the big pyramid was built as 8485e inches. 8485e inches is 21553 cm, 27 cm difference. {1.25+ppt} — ( Pi/2 squared * 105 = 259.08 )
(Now 2022, perhaps in March, I saw a TV program about the pyramid of the sun and the pyramid of the moon and the general area and the presenters claimed that a new unit called the TIM (i think it was called) had been found and its length was 83 centimeters. They said it was the length from shoulder to fingertips.)
————————————————
Xs, Cs, Meeting points
C1 is the centre of P1, and C2 and C3 are the centres for P2 and P3. Three points make a circle, and the centre of the circle for C1 C2 C3 is at Cs at latlon 29.963100 31.150112 . Just as X13 is the intersection of lines from opposite ends of the diagonals of P1 and P3, there are X12 and X23. The centre for X13 X23 X12 is at Xs at latlon 29.984159 31.117526 The distance from Cs to Xs is 4723.7 My which is close to 4714e, 4*es8. It’s out by about 26 feet in two and a half miles. I wanted to see what configuration would make the distance exactly 4714e, so I moved the centre of P2 around, and lengthened and shortened the sides gradually each time I moved it. Out of all the possibilities, one was lengthening the sides to 6*sqrt(2) inches, and moving the centre just under 5.5 inches somewhere towards the north and west. [ 20170202 This also makes the number HighLow take the value 23.57e. There seem to be thousands of points where this happens, or might happen, that is where both distances might be exact, but they all seem to be less than 1/100 inch apart from each other. By points I mean positions for the centre of P2. I need a more refined technique ]
Just as X13 X12 and X23 are crossing points, M12 M23 and M13 are meeting points. Where X is for a crossing point the M is for a meeting point. Whereas the X points are made using ‘opposite’ ends of diagonals, the M points are made by using ‘same’ ends of the diagonals.


The Jerusalem temple and the Baalbek ruins both have stones that are so big and heavy that it looks like nobody could possibly have put them there.
The direct distance from M13 to the Baalbek ruins is 408.18- miles 1/sqrt(6), and going on straight through from the Baalbek ruins to google’s Mount Ararat point it’s 3144… feet, looks like pi for what it’s worth, which is almost certainly nothing, but I’m not leaving it out, I’m leaving it in for people who like sich things. I had a bit of a look around and the line from St Catherine’s Abbey on Mt Sinai (maybe Mt Sinai) through the Jerusalem temple to the Baalbek ruins is very nearly straight and the distance from St Catherine’s Abbey to the Jerusalem temple is 235.07 miles and the distance from the Jerusalem temple to the Baalbek ruins is 318333 My which looks like 1/pi. I know that these distances can be coincidences in the same way that people are always finding extra ley lines that aren’t real ones, or as people find patterns in ufo paths in the sky. It all depends whether you think it’s intended. I then used maybe twenty sites in the middle east, some chosen distances (as strings), and about the same number of randomly generated distances (as strings), and found nothing worth mentioning from the random numbers, and the few things below from the chosen distances, none of which is interesting, except maybe the second one. I’m happy to leave such things, and their statistics, to somebody else. C2 to M13 4081 feet X12 to M12 23558 feet Xs to M12 272059 inches M12 to Karnak 17335118 inches C2,C1,X23,X12,X13 and head_of_sphinx to Jerusalem_temple are all within 1ppt of sqrt(3) (times 10 million) inches. M13 to Nippur is 848 miles, but I think that’s the new Nippur, and I’m really only including all this to show that there doesn’t seem to be anything that seems obviously significant.

The line M12 M13 M23 (has to be a straight line by geometry) has a bearing of from about 45.02 to 45.04 degrees, and the line through Xs and Cs has a bearing of about -53.26 degrees (close to the angle in a 3-4-5 triangle). The M12 M13 M23 great circle misses Baalbek_ruins by about 6 km via the northwest, and probably would’ve missed it by more (rather than less) some thousands of years ago, that is if the plates are moving the way I think they are, but I don’t know. I’m assuming that the giant blocks of stone at Baalbek weren’t put there by Romans, but sometime before them. There are also unliftable stones at the Jerusalem temple, mentioned above.
————————————————
‘Ley’ line
A line through Burrowbridge Mump through Glastonbury Tor to the Avebury circle has a bearing of about 61.3 or 61.4 degrees. This line is mostly known as the St Michael’s ley line. The three places mentioned are the ones that involve alteration of the land, and their alignment looks deliberate, especially considering the orientation of the first two, that is Burrowbridge Mump and Glastonbury Tor are shaped so that the line goes along close to their long axes.





Maltese cross, mostly for fun
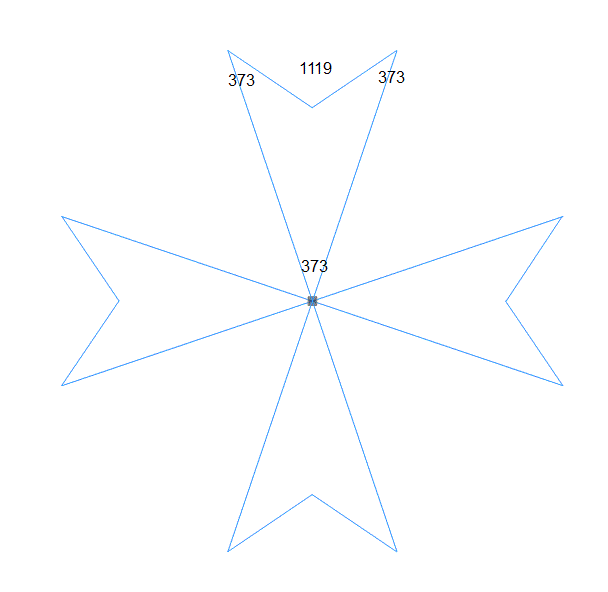
Some isolated things.
The distance from the centre of the Rollright Stones to the nearby “Whispering Knights” is sqrt(2) inches (times 10000). The distance from the Stenness stone circle centre to Maes-Howe is 3847.65 feet. There may be many more such things – there are a lot of ancient stone circles and mounds, and there’ll be a lot of coincidences (like an excess of ley lines). Maybe many stone circles are copycat circles. I think there might be an My grid around Newgrange.
————————————————
It’s been claimed that the meridian at P1 divides the land area of the world in half, but according to my labours there are a dozen or more such meridians, and they all occur somewhere between longitudes 29.26 and 29.51, that’s about 112 to 130 miles west roughly. Similarly the dividing latitude is at about latitude 22.9 north roughly. These figures are based on coastline points that might be several miles out here and there one way or the other maybe, but anyway, there doesn’t seem to be such a dividing meridian through the Great Pyramid. I used ‘World Vector Shoreline’ (thank you Renzo), and joined the dots.
————————————————
The Last Thing
Did aliens build the pyramids !? -:) During the last couple of decades NASA used orbiting spacecraft to measure the surface gravity of the moon, and says it’s a mean of 1.622 m/sec^2. Prior to that its estimate was 1.61 m/sec^2. Now a pendulum of length equal to the height of P1 has a period of 60 seconds in a gravitational field of 1.608 m/sec^2, which rounds up to 1.61 m/sec^2, the same as the ground based estimate. If aliens were the Builders, you’d think they’d know the 1.622 m/sec^2 measurement, and the inch would have to be a bit longer. Therefore the Builders weren’t aliens. Hah.
Sure gives you something to think about.
————————————————
During my travels through these numbers, up many tributaries, every now and then, quite often really, I came across what I think is a new approximation for Pi which is Pi ~ 20*sqrt(2)/9 Well, it’s closer than 22/7 anyway.
John W. Gerson